Hairpin vortex organization in wall turbulence
Categories: Journal
Author: Ronald J. Adrian Year: 2007
==Coherent structures in wall turbulence transport momentum and provide a means of producing turbulent kinetic energy.== Above the viscous wall layer, the hairpin vortex paradigm of Theodorsen coupled with the quasistreamwise vortex paradigm have gained considerable support from multidimensional visualization using particle image velocimetry and direct numerical simulation experiments. Hairpins can autogenerate to form packets that populate a significant fraction of the boundary layer, even at very high Reynolds numbers. The dynamics of packet formation and the ramifications of organization of coherent structures hairpins or packets into larger-scale structures are discussed. Evidence for a large-scale mechanism in the outer layer suggests that further organization of packets may occur on scales equal to and larger than the boundary layer thickness.
Break the complex, multiscaled, random fields of turbulent motion down into more elementary orga- nized motions that are variously called eddies or coherent structures.
The total shear stress is a sum of the Reynolds shear stress $−\rho uv$ and the viscous stress, $\tau (y) = -\rho uv + \mu \frac{dU}{dy}$.
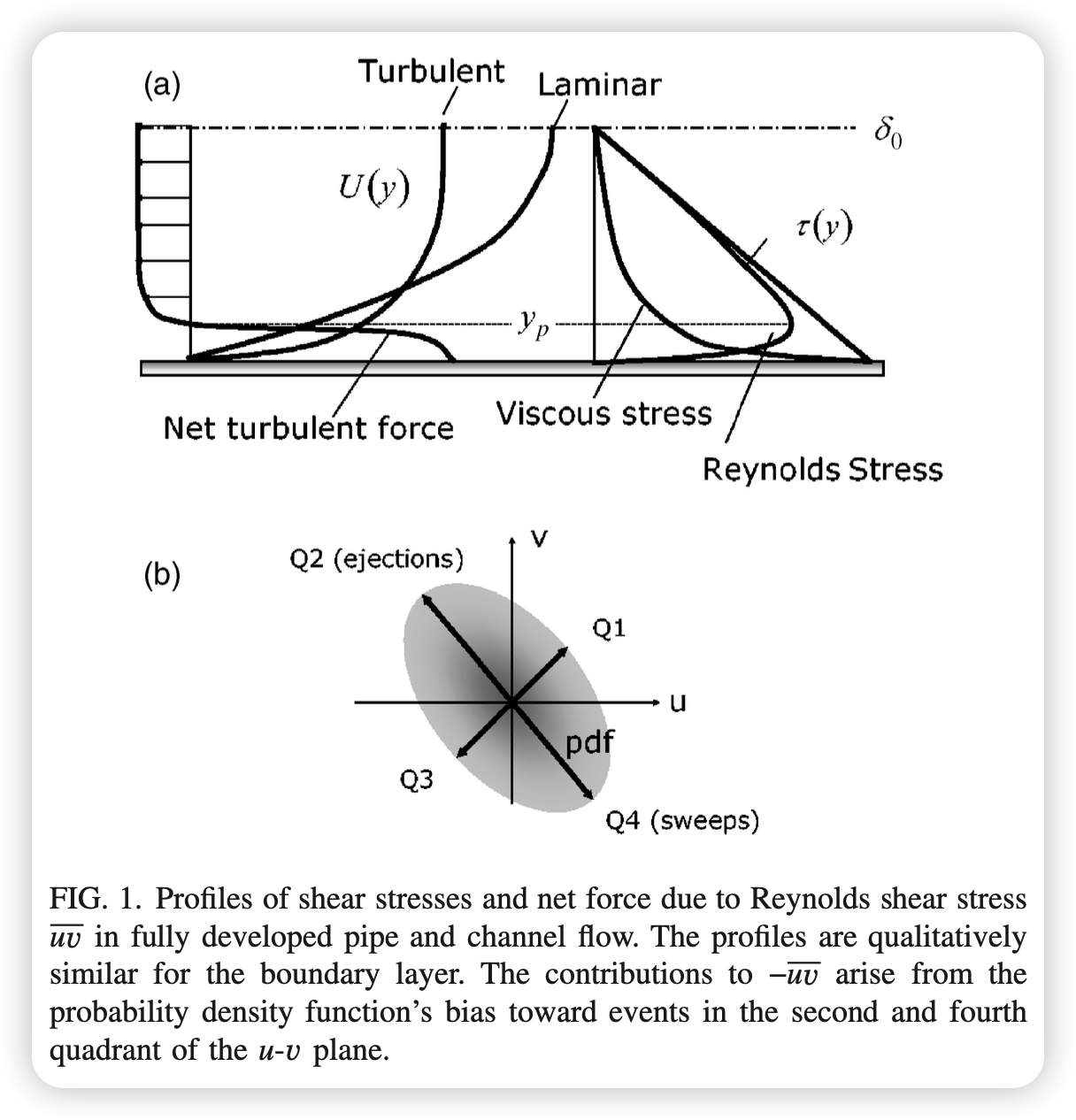
in Fig.1 the net force must be negative and roughly constant above $y_p$ and positive below $y_p$. In this way, mean transport of turbulent momentum represented by the net Reynolds force retards the mean velocity in the core of the flow and accelerates it near the wall. The increased mean velocity near the wall causes the gradient of the mean velocity to increase, leading to higher wall shear stress.
Because of the leading role Reynolds stresses play as the first unclosed quantities in the hierarchy of Reynolds mo- ment equations, the foremost question in wall turbulence concerns the mechanisms responsible for creating Reynolds shear stress. That is, what specific eddy motions cause the u and v components to be anticorrelated and to vary as ob- served? It is well known that the probability density function of the $u$ and $v$ fluctuations behaves qualitatively as shown in Fig. 1, with more probability of spending time in the second Q2 and fourth Q4 quadrants of the $u-v$ plane, so that the average of u times v is negative. Events in the second quad- rant correspond to negative streamwise fluctuations being lifted away from the wall by positive wall-normal fluctua- tions, and they are referred to as ejections. Events in the fourth quadrant correspond to positive streamwise fluctua- tions being moved toward the wall. They are associated with motions called sweeps. Quadrant analysis of this type does not explain the form of the eddies creating sweeps and ejec- tions, but it does permit evaluation of the contributions these events make to the total mean values of various quantities such as kinetic energy, dissipation, etc.
